Value at Risk: Variance & Volatility
We calculate daily volatility as the standard deviation of the daily percentage change (= daily returns) of the stock price. Our implmentation for returning the daily percentage change is defined in the class PercentageChange.java
We explore a number of ways of estimating volatility:
- Equal Weighted
- Exponentially Weighted Moving Average
- GARCH(1,1)
Each have their of trade-offs, complexity being the main one. But nonetheless, they all return an estimate of volatility.
Volatility is the square root of the variance.
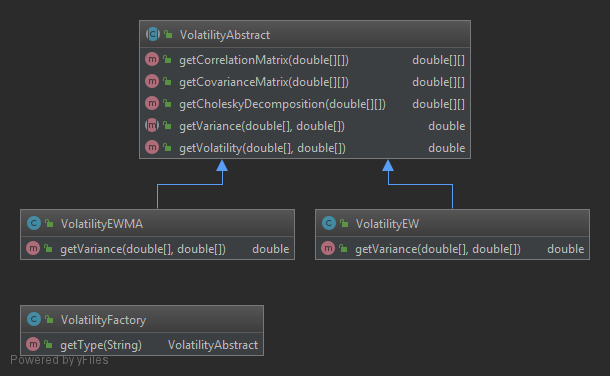
VolatilityAbstract.java defines the abstract method getVariance()
The concrete method getVolatility() is defined as:
public double getVolatility(double[] xVector, double[] yVector) {
double variance = getVariance(xVector, yVector);
return Math.sqrt(variance);
}
We have three concrete classes that implement this method:
VolatilityEW.javaVolatilityEWMA.javaVolatilityGARCH.java
VolatilityFactory
Before we can return volatility, we must construct a VolatilityFactory.
This is a class that contains a method that allows us to instantiate the correct concrete class.
public class VolatilityFactory {
public VolatilityAbstract getType(String type) {
if (type == null)
return null;
if (type.equals("EW"))
return new VolatilityEW();
if (type.equals("EWMA"))
return new VolatilityEWMA();
if (type.equals("GARCH"))
return new VolatilityGARCH();
return null;
}
}
So to return an estimate for volatility with equal weighting, we could write:
double volatility = new VolatilityFactory()
.getType("EW")
.getVolatility(returns1, returns2);
where returns1 and returns2 are vectors of percentage changes.
Equal Weighted Variance
The squared volatility (=variance) can be calculated using a simple weighted model:
\[\sigma^2_n = \frac{1}{m}\sum_{i=1}^m u^2_{n-i}\]That is, we square each percentage change and return the average of all these elements.
public class VolatilityEW extends VolatilityAbstract {
@Override
public double getVariance(double[] xVector, double[] yVector) {
double sum = 0.0;
int elements = xVector.length;
for (int i = 0; i < elements; i++)
sum += (xVector[i] * yVector[i]);
return sum /elements;
}
Exponentially Weighted Moving Average
In estimating daily volatilitym it makes sense to assume that more recent observations are more relevant than those in the past. But the trade off is that we want to include as many observations in our calculations as possible. Excluding older observations would go against that.
We consider a weighted model in which the weights decrease exponentially for older observations:
\[\sigma^2_n = \lambda \sigma^2_{n-1} + (1-\lambda) u^2_{n-1}\\ \text{where } \lambda = 0.94\]Once again we iterate through our vector of squared percentage changes \(u^2\), moving from oldest to newest observations. This is a recursive forumla. The next estimate for volatility \(\sigma_n\) depends on the previous estimate \(\sigma_{n-1}\).
Our weighting is defined as \(\lambda = 0.94\) which is what J.P. Morgan uses in their RiskMetric platform.
public class VolatilityEWMA extends VolatilityAbstract {
private static double lambda;
static {
// Per JP Morgan's RiskMetrics
lambda = 0.94;
}
@Override
public double getVariance(double[] xVector, double[] yVector) {
int elements = xVector.length;
double EWMA = xVector[elements - 1] * yVector[elements - 1];
for (int i = 1; i < elements; i++)
EWMA = (lambda * EWMA) + ((1-lambda) * xVector[elements -1 - i]* yVector[elements -1 - i]);
return EWMA;
}
}
GARCH(1,1)
The Generalised Autoregressive Conditional Heteroskedastic process, GARCH(1,1), is an extension of EWMA that introduces a weighted \(\gamma\) long-term average variance \(V_L\).
\[\sigma_n^2 = \omega + \alpha u^2_{n-1} + \beta \sigma_{n-1}^2\\ \text{where } \omega = V_L\]where the parameters \({ \alpha, \beta, \omega }\) are to be found via maximum-likelihood estimation, using an optimisation algorithm such as Levenberg-Marquardt.
public class VolatilityGARCH extends VolatilityAbstract {
private static double alpha, beta, omega;
static{
alpha = 0.08339;
beta = 0.9101;
omega = 0.000001346;
}
@Override
public double getVariance(double[] xVector, double[] yVector) {
int elements = xVector.length;
double uSquared[] = new double [elements];
double sigmaSquared = uSquared[0];
for (int i = 1; i < uSquared.length;i++)
sigmaSquared = omega + (alpha*uSquared[i]) + (beta*sigmaSquared);
return sigmaSquared;
}
}